三角比について、「何のために学ぶのだろうか?」と頭を悩ます学生は多いと思います。
三角比は、将来的に数Ⅱで学ぶ三角関数の基礎となります。
なお、社会に出てから仕事で三角関数を使うこととなり、基礎である三角比から学び直さなければならず、大変な思いをするという人が案外多いのです。
中でも三角比の正弦定理と余弦定理は測量現場で使われることが多く、正確な日本地図作製のために用いられた学問としても有名です。
本記事では、数学講師が正弦定理・余弦定理の公式、証明を例題を用いて、なるべくわかりやすく解説します。
正弦定理とは?どこを表すもの?
正弦定理とは、三角形の正弦(sinθ)の比は3辺の長さの比に等しいというものです。つまり、△ABCにおいて、sinA:sinB:sinC=a:b:c が成り立ちます。
また、三角形の外接円の半径をRとすると、1つの辺の長さとその向かいあう角の正弦との割合は2Rで一定となり、次の等式が成り立ちます。
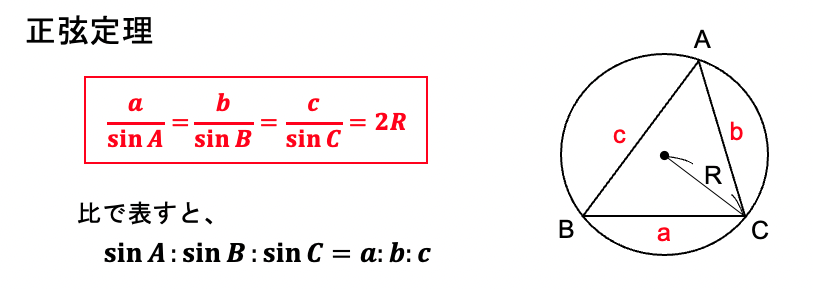
関連記事:三角比を数学講師がわかりやすく解説!覚え方・公式・表まで
正弦定理の証明をわかりやすく解説
正弦定理の証明には、円周角の定理と、円に内接する四角形の性質を利用します。
【円周角の定理】
(1)1つの弧に対する円周角の大きさは中心角の半分
(2)同じ弧に対する円周角の大きさは等しい
【円に内接する四角形の性質】
円に内接する四角形の対角の和は180°
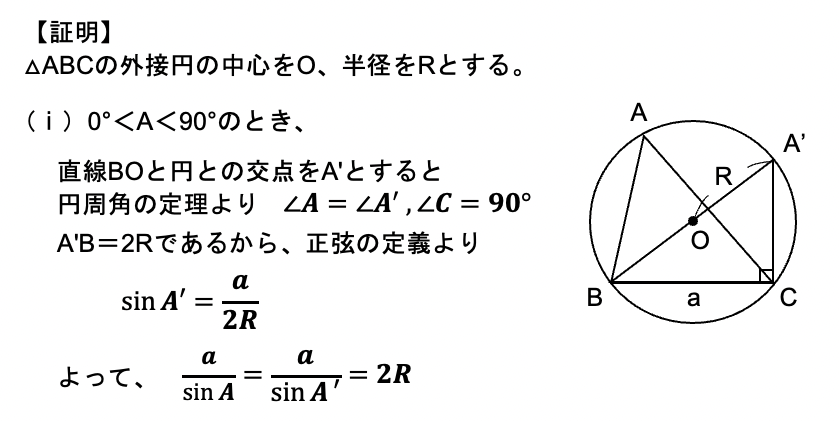
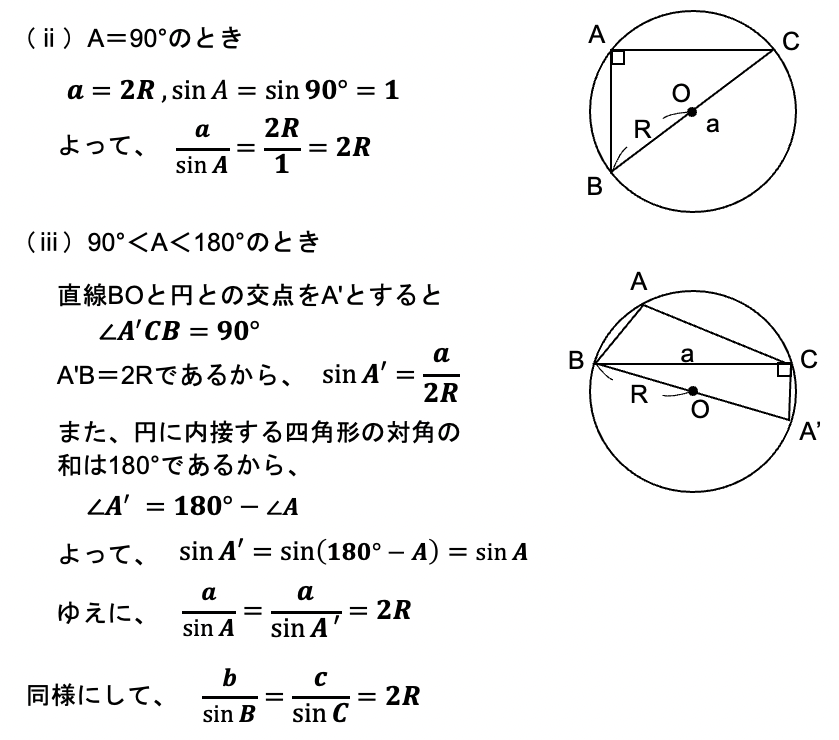
証明は、鋭角三角形、直角三角形、鈍角三角形に場合分けして行います。
正弦定理の例題
正弦定理は問題に応じて必要となる等式を取り出して使います。
また、2つの角が分かっている場合は、三角形の内角の和は180°を用いて、残りの角を求めることができます。例題として次の問題を見てみましょう。
【問1】△ABCにおいて、a=10,A=45°,C=75°のとき、B,b,Rを求めよ。ただし、Rは内接円の半径とする。
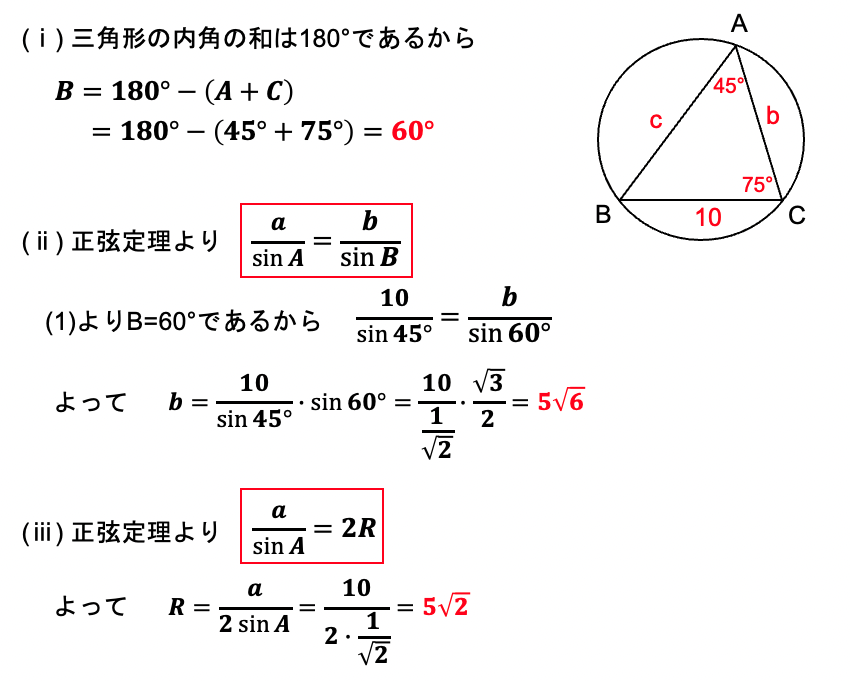
このように、正弦定理の必要な等式を取り出して、分かっている値を当てはめていくと、それぞれの値を求めることができます。
なお、この問題では、cの長さを求めようとすると、sin75°の値が分からないので解くことができませんが、下記の余弦定理と組み合わせることで求めることができます。(【問3】参照)
余弦定理とは?かんたんに理解しよう
余弦定理とは、三角形の2辺と1角が分かっている場合、残りの辺の長さを求めることができる公式です。
あるいは、3辺が分かっている場合、余弦(cos)を求めることもできます。
次の3つの等式が成り立ちますが、位置関係さえ理解すれば、どれか1つ覚えれば十分です。
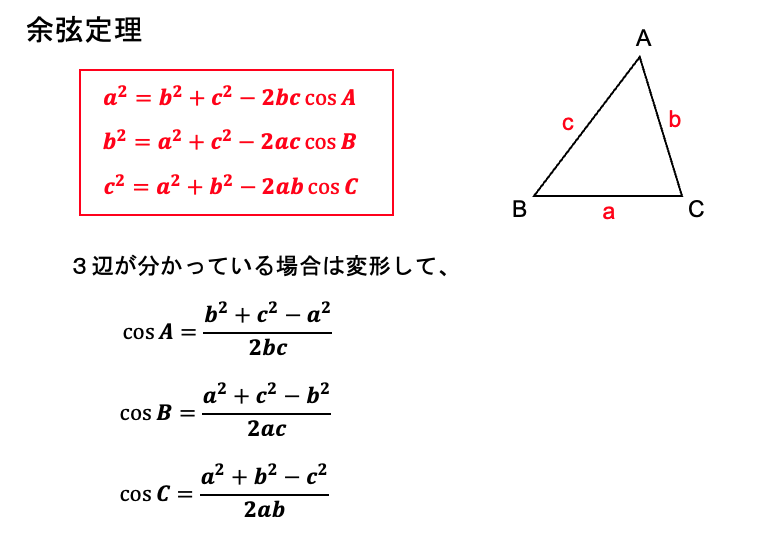
なかなか覚えにくい公式ですが、前半(a2=b2+c2 )の部分は三平方の定理と同じ形で、これに(-2bccosA)を加えたものが余弦定理となります。
A=90°の場合、cos90°=0より、 -2bccosA=0となり、a2=b2+c2が成り立ちます。つまり余弦定理とは、三平方の定理を直角三角形以外の三角形に拡張したものと言えます。
余弦定理の証明をわかりやすく解説
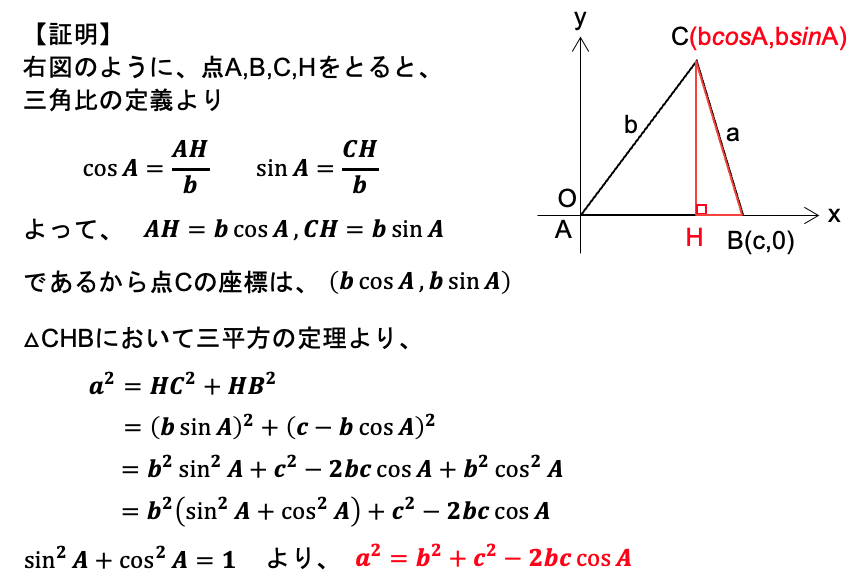
a2=b2+c2-2bccosAを証明してみましょう。(他も同様に証明できる)
下図のように、xy平面上に△ABCの点Aを原点、点Bをx軸上、点Cをx軸の上側にとる。点Cの座標は(bcosA,bsinA)と表すことができる。点Cからx軸に垂線CHを下ろし、△CHBに三平方の定理を適用する。
余弦定理の例題
2辺1角または3辺が与えられたときは余弦定理を利用します。
【問2】
(1)△ABCにおいて、a=7,c=8,A=60°のとき、bを求めよ。
(2)△ABCにおいて、a=7,b=15,c=13 のとき、Cを求めよ。
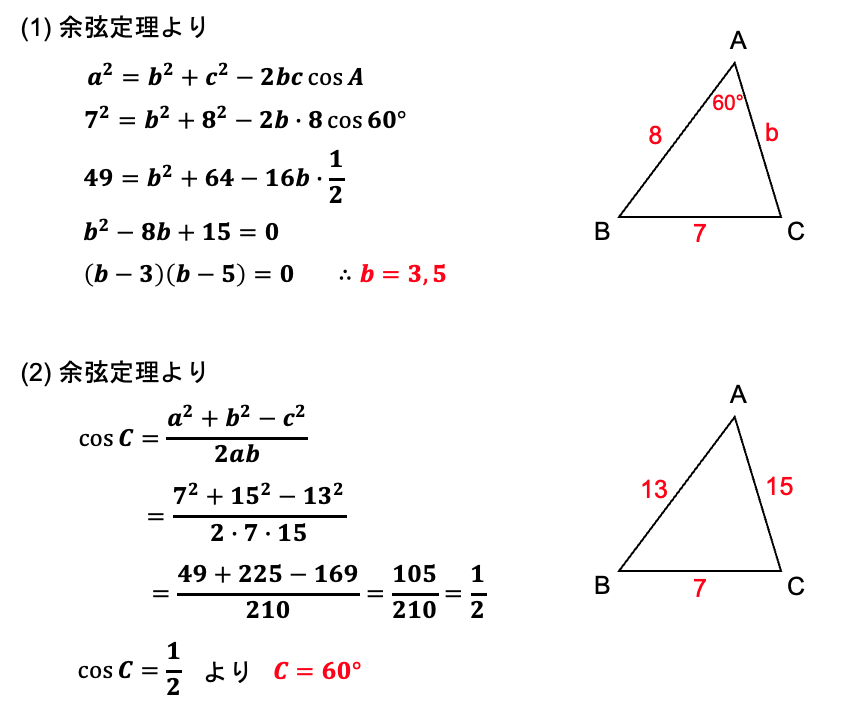
(1)は2辺1角が分かっているので、与えられているAを使ってcosAを含む余弦定理を適用すれば、bの2次方程式が得られます。これを因数分解あるいは解の公式を使って解けば、bを求めることができます。この問題のように、2次方程式の解がどちらも正の数の場合は解が1つに決まらず、2つの場合もあります。
(2)は3辺が分かっているので、求めたいCを含んでいるcosCの余弦定理を適用すれば、cosCを求めることができます。もしCが30°や45°といった有名角であれば、角度まで求めることができます。
正弦定理・余弦定理の活用
上の【問1】で、cの長さを求めようとすると、sin75°の値が分からないので解くことができませんでした。
そこで、正弦定理と余弦定理を駆使して、sin75°やcos75°を求めてみましょう。
【問3】頂角が30°の二等辺三角形を利用して、sin75°とcos75°を求めよ。
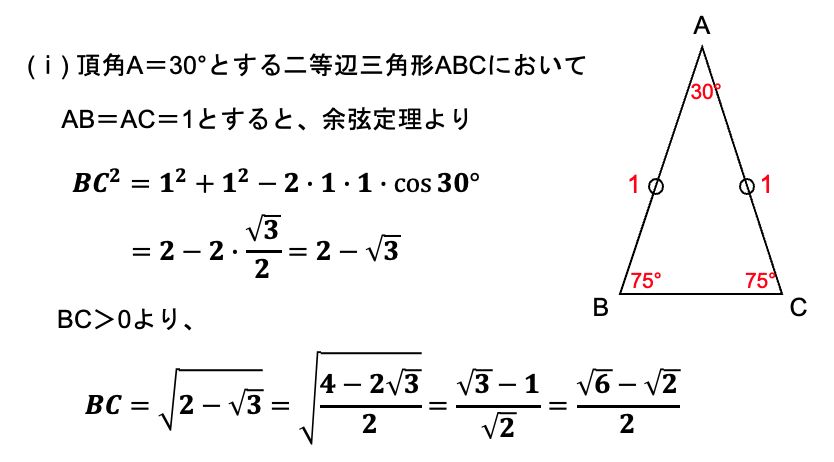
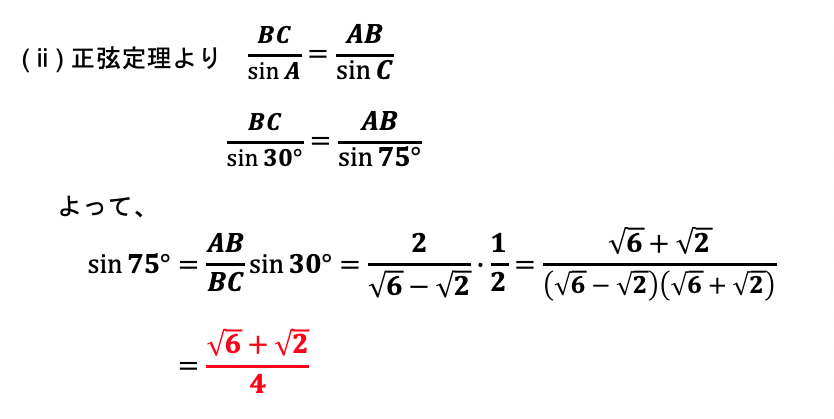
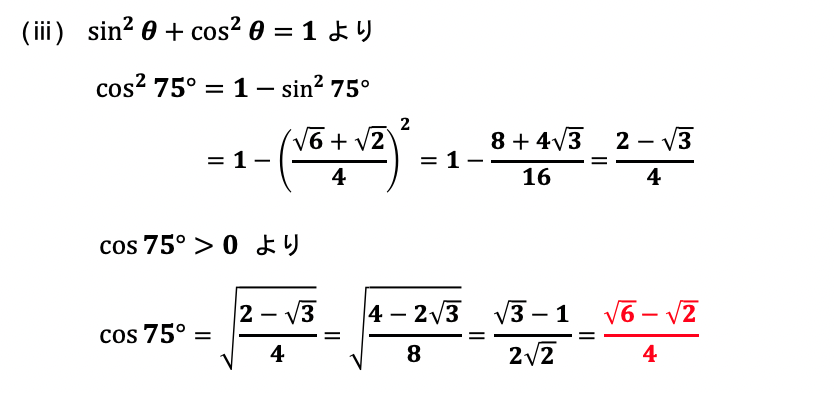
この問題は、正弦定理・余弦定理の他、三角比の公式や二重根号の解消、有理化など、数学Ⅰの基礎が詰まっていますので、大学入学共通テストに出そうな問題です。
なお、sin(90°-θ)=cosθの性質を利用すれば、sin75°=cos15°であり、sinとcosの関係式より sin15°も求めることができます。よって、有名角の30°,45°,60°と合わせて、15°の倍数の三角比はすべて求めることが可能です。
また、ここでは割愛しますが、【問3】と同様に頂角が36°の二等辺三角形を考えると、cos36°やcos72°といった18°の倍数の三角比も数学Ⅰの範囲内で求めることができますので、やってみて下さい。
さいごに
正弦定理・余弦定理は公式も複雑で、苦手意識を持つ生徒も多いと思います。
重要なのは、”公式を丸暗記すること”ではなく、忘れても導けるように”本質を理解すること“です。
ほんのちょっとした捉え方の違いで、数学力はグッと身につきます。
個別指導塾の「好文館」では日本全国を対象に、三角比の他、数学の基礎をオンラインにて個別指導しております。
お問い合わせ後、お電話やZoomにて学習の進み具合や弱点などを教えてください。




