大学入試共通テストとは、国内の大学に入学する際に、多くの国公立大学や一部の私立大学で利用される全国規模の学力試験です。
その中でも「数学ⅠA」は文系の学生も含めて多くの受験生が選択する科目です。
「数学ⅠA」は70分 100点で大問の構成及び配点は以下の通りです。(2025年時点)
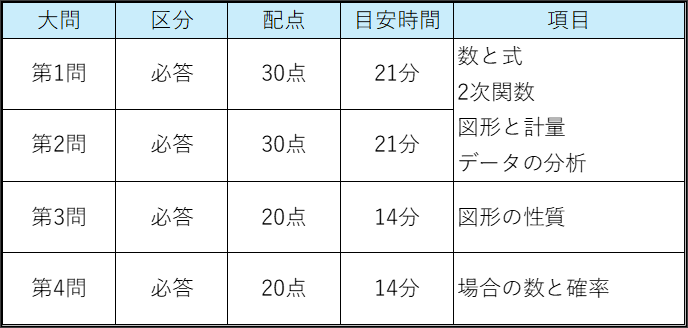
2025年から、選択問題であった「整数の性質」がなくなり、「図形の性質」と「場合の数と確率」が必答となりました。2024年以前は半数を超える受験生が整数と確率を選択していましたので、図形問題のウエイトが高まったと言えます。
この記事では、共通テスト攻略のポイントとして数学Ⅰの「数と式」について解説します。
「数と式」は高校数学の基礎となるもので、最も重要な単元です。
共通テストの得点アップを狙う上で特に重要な、下記の項目についてはおさえておきましょう。
・因数分解
・不等式
・無理数
・絶対値
過去に出た問題などを参考にしながら解説していきます。
因数分解
式の展開は公式を覚えていなくても1つずつ分配すれば必ずできるとして、因数分解はある程度のコツを理解する必要があります。
たとえば次のような問題を見てみましょう。

因数分解の基本は共通因数をくくりだすことです。
例題1は4x2-1が(2x-1)(2x+1)と因数分解できることから、あとの16x-8から(2x-1)または(2x+1)が作れないかと考えます。すると(2x-1)が共通因数であるから、解答のように解くことができます。
また、次のような因数分解もノーヒントで解けるようにしておきましょう。
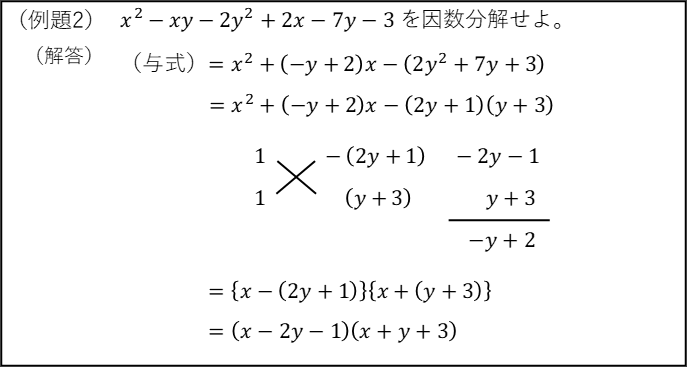
手順は以下の通りです。
① xについて(あるいはyについて)降べきの順に並べる。
② 定数項(この場合はxを含まない -2y2-7y-3)を因数分解し、積の形にする。
③たすき掛けの因数分解を考える。x2の係数1×1と、定数項(2y+1)×(y+3)の組み合わせで(-y+2)を作り出すことができれば、因数分解可能である。
この手の因数分解は、不等式や領域(数Ⅱ)などの問題に応用されることがあります。
不等式
1次不等式はほとんど方程式と同様に解くことができますが、負の数を掛ける(割る)ときは不等号の向きが逆転することに注意が必要です。
たとえば、(3-π)x<0 を解く場合、π≒3.14であるから、3-π<0 です。よって、両辺を(3-π)で割るとx>0 が解となります。
そのため次の例題のように、正負が分からない文字定数で割るときは、場合分けが必要となります。

(ⅰ)aが正の数のときはそのまま両辺を aで割ればよい。
(ⅱ)a=0のときは (左辺)=0となるため、xの値に関わらず不等式が成り立つ。
(ⅲ)aが負の数のときは両辺を負の数で割ることになり、不等号の向きが逆転する。
2次不等式について詳細は「2次関数」で扱いますが、ここでは下記を覚えていれば十分でしょう。
(x-α)(x-β)<0 ⇔ α<x<β
(x-α)(x-β)>0 ⇔ x<α,β<x (ただし、α<β)
上記のように因数分解できない場合は、2次方程式の解をα,βとすればよいです。
(∵因数分解を無理数まで拡大すると必ず(x-α)(x-β)と表すことができる(例題4参照))
無理数
特に重要なのは無理数がどのくらいの数であるか把握することです。
たとえば、√2という数は、√1<√2<√4であり、1と2の間の数であることが分かります。
そうすると、2√2という数は、1<√2<2の辺々を2倍すると、2<2√2<4となりますが、これでは不十分なことがあります。このようなときは先に、2√2=√8としておいて、2<√8<3とするとさらに絞り込むことができます。
(逆に考えると、2<√8<3の辺々を2で割ると、1<√2<1.5であることが分かります)
テストでよく出るのが、与えられた不等式を満たす整数解はいくつあるかという問題です。

まずは上述の手順で因数分解を行います。①の(左辺)=0の解は、x=5,1+2√2となります。
ここで、5と1+2√2の大小関係が必要になってきます。上記の通り1+2√2は3と4の間の数であることから、1+2√2<5であることが分かり、解が得られます。
絶対値
絶対値の基本は、絶対値の中が正の数(または0)のときはそのまま絶対値を外し、負の数のときはマイナスをつけて外すことです。つまり
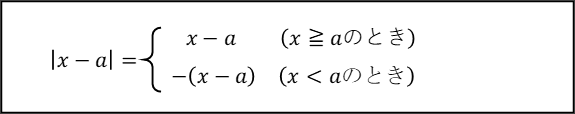
これが基本となりますので、絶対値の中に変数があれば場合分けが必要となります。
絶対値を含む不等式については、下記を覚えておきましょう。
|x|<a ⇔ -a<x<a
|x|>a ⇔ x<-a,a<x (ただし、a>0)
例題を見てみましょう。

この例題でまず重要なことは、根号の中を因数分解すると根号が外せるわけですが、√a≧0であることから、絶対値が付きます。つまり、√a2=|a| です。
|x+1|は-1を境に符号が変化し、|2x|は0を境に符号が変化するわけですから、解答のように3通りに場合分けが必要となります。
たとえば(ⅱ)-1≦x<0 の範囲であれば、x+1≧0、2x<0であることから、x+1>-2x を解けばよいことになります。
あとは、それぞれの場合で式を当てはめて不等式を解けばよいのですが、求めた解の範囲が条件を満たすのか満たさないのか、あるいは一部だけ満たすのかを確認する必要があります。
この場合、(ⅰ)は条件を満たさず、(ⅱ)(ⅲ)は条件の一部を満たすこことなり、(ⅱ)(ⅲ)で得られた範囲を合わせて、解答の通りとなります。
さいごに
今回は共通テスト対策として「数と式」に焦点を当てて、因数分解、無理数から絶対値を含む不等式の問題まで紹介しました。
数学が苦手!という生徒は「数と式」でつまづいていることが多いように思います。特に場合分けの必要性が分からないという生徒が多くみられます。場合分けの必要性が理解できれば、解ける問題も増えてきて、問題が解けるようになると数学が面白くなると思います。
ほんのちょっとした捉え方の違いで、数学力はグッと身につきます。
個別指導塾の「好文館」では日本全国を対象に、数学の基礎をオンラインにて個別指導しております。
お問い合わせ後、お電話やZoomにて学習の進み具合や弱点などを教えてください。




